A low overhead flow-holding algorithm in software-defined networks【3】
3.2 Cost Function
The cost function is a piecewise function used to simulate the nonlinear impact of a link load on the network congestion in internet traffic engineering [10,26]. As shown in [10], we can use the cost function (7) to simulate the nonlinear impact of the flow table usage increase on the controller’s workload.
The cost function is used for all switches, and p is the utiliza- tion of the flow table on each switch. With the increasing number of the entries installed on the switches, the value p also increases.
3.3 Problem Function
The problem of reducing and balancing flow table entries in SDN switches to hold more flows with low overhead in SDNs is formulated as:
The Eq. (8) is the objective function to reduce and balance the flow entries in SDN switches by minimizing the cost function for all switches. It should satisfy the Constraints 1 to 4.
3.4. Complexity analysis
The cost function g(p) is a integer linear function, then our problem can be reduced to the Mixed-integer programming problem. So our optimization problem is at least as hard as Mixed- integer programming problem. The Mixed-integer programming problem is an NP-hard problem, so the problem of reducing and balancing the flow entries in SDN switches to hold more flows with limited resources is also NP-hard. The solution space of our problem is O(2|V||F|), where |V| is the number of nodes in the net- work, |F| is the number of flows in the network.
Therefore, to efficiently solve the problem, we propose a greedy algorithm to approximate optimal results.
4 Heuristic Algorithms
Section 3 shows that the problem is an NP-hard problem. We propose the KSGT algorithm to get the approximate optimal re- sults. In this section, KSGT firstly divides all flows into some clus- ters based on the coincidence degree of the forwarding paths of the flows. Secondly, KSGT greedily selects a small number of switches from the forwarding path to install entries. Moreover, KSGT just greedily enumerates the possible schemes of the flows in each cluster to achieve the optimal solutions of the cluster. So the KSGT does not have high time complexity because it does not enumerate all of the solution space. Finally, we use a phase func- tion to balance the flow table entries of different switches. Hence, KSGT can effectively reduce and balance the flow table entries of switches to hold more flows even though many new flows arrive in the network at the same time.
4.1 The Outline Of The KSGT Algorithm
The cluster-k denotes the flows in the k-th cluster. The flows in the same cluster have high coincidence degree of forwarding paths. We use the scheme(cf) to denote the optimal schemes of installing flow entries for flow cf, for example, s1 and s7 is a scheme for flow cf in Fig. 2. We use scheme-cluster(k) to indicate some opti- mal schemes for flows in the k-th cluster. The inputs of KSGT algo- rithm are the network G = (V , E ) and the node vector of each flow, the output is the number of entries to be installed for all flows and the corresponding nodes. The Algorithm 1 has four phases: the first phase is to classify the flows according to the number of overlapping nodes by K-Similar algorithm; the second phase greed- ily select schemes for each flow; the third phase is to use the cost function to evaluate the possible schemes of the flows in each clus- ter to achieve some optimal solutions for every cluster; the fourth phase is to combine every two clusters into one until only one re- mains. Then we can get the optimal results by the Algorithm 1.
4.2. Phase 1: flow classification
The inputs of Algorithm 2 are the network G = (V,E) and the flow set F. The outputs are k clusters, and the flows in each cluster. The algorithm is similar to the k-means algorithm [15]. As shown in the Algorithm 2, the center of each cluster is set in the line 1– 3. KSGT divides all flows into clusters based on the coincidence degree of the forwarding paths of the flows. In our experiment, we analyzed a large number of topologies and traffic, each cen- ter of the clusters will not exceed ten nodes. Therefore, we set the number of nodes in the cluster center vector to be less than ten. We need to calculate the coincidence degree of the nodes in each cluster as the cluster center vector. So the more flows in the clus- ter, the higher the computational complexity required. The lines 5–7 put each flow into the corresponding cluster according to the number of overlapping nodes, and the function number(f△ck) cal- culates the number of overlapping nodes between flows vector f and flows vector ck. If flow f has the equal function value with the center vector of cluster j and cluster k we map it to the smaller cluster. We recalculate each center vector of the clusters in line 8-10. Line 4 means that the algorithm breaks and returns the results when there is no significant change in the clusters.
4.3 Phase 2: routing a single flow f
The input of the Algorithm 3 is the node vector cf of the flow f, the output is the schemes of the flow f. Line 2 means that it se- lects the first node to install an entry. Line 3 sets up the maximum number of MPLS labels. Line 4 insures that it selects two schemes whose nodes do not completely coincide. In line 5–8, it greedily selects one scheme to install flow entries for the flow f. In line 9, it records the scheme, and then the number of MPLS labels minus 1 in line 11. For example, in Fig. 2, the schemenodes={s1,s7} is one scheme of flow f.
 |  |
分享让更多人看到 
推荐阅读
相关新闻
- 评论
- 关注























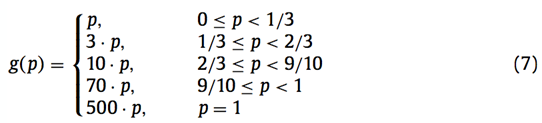








 第一时间为您推送权威资讯
第一时间为您推送权威资讯
 报道全球 传播中国
报道全球 传播中国
 关注人民网,传播正能量
关注人民网,传播正能量